Manually Tuning a Fuji Temperature Controller
Back to PXR3
Back to PXR4
Back to PXR5
Back to PXR7
Back to PXR9
Back to PXG Series
Manually Tuning Your Fuji Temperature Controller
Tuning
Tuning Fuji Temperature Controllers, as with any PID loop, requires tuning each parameter separately and in sequence. To achieve good PID temperature control manually, you can use the trial and error method explained below.
Tune the Proportional Band
Set Integral Time = 0 (off)
Set Derivative Time = 0 (off)
Start with a large Proportional Band value which gives very sluggish control with noticeable offset and tighten by decreasing the value in half. Analyze the process variable. If the control is still sluggish, tight-en by decreasing the value in half again. Continue with the same procedure until the process starts to oscillate at a constant rate. Widen the Proportional Band by 50%, or multiply the setting 1.5 times. From a cold start, test and verify that the Proportional Band allows maximum rise to setpoint while maintaining minimum overshoot and offset. If not completely satisfied, fine-tune the value, up or down, as needed and test until correct. The Proportional Band is now tuned.
Add Integral Time
Start with a large Integral Time value which gives very sluggish response to process offset and tighten by decreasing the value in half. Analyze the process variable. If the response to process offset is still sluggish, tighten by decreasing the value in half again. Continue with the same procedure until the process starts to oscillate at a constant rate. Increase the Integral Time value by 50%, or multiply the setting 1.5 times. From a cold start, test and verify that the Integral Time allows maximum elimination of offset with minimum overshoot. If not completely satisfied, fine-tune the value, up or down, as needed and test until correct. The Integral Time is now tuned.
Add Derivative Time
Do not add Derivative Time if the system is too dynamic. Start with a small Derivative Time value which gives sluggish response to process upsets and double the value. Analyze the process variable. If the response to process upsets is still sluggish, double the value again. Continue with the same procedure until the process starts to oscillate at a quick constant rate. Decrease the Derivative Time value by 25%. From a cold start, test and verify that the Derivative Time value allows maximum response to process disturbances with minimum overshoot. If not completely satisfied, fine-tune the value, up or down, as needed and test until correct. Note that the Derivative Time value is usually somewhere around 25% of the Integral Time value.
Another tuning method is the closed-loop cycling or Zeigler-Nichols method. According to J.G. Zeigler and N.B. Nichols, optimal tuning is achieved when the controller responds to a difference between set-point and the process variable with a 1/4 wave decay ratio. That is to say that the amplitude of each successive overshoot is reduced by 3/4 until stabilizing at setpoint.
Procedure Step by Step
- Integral Time=0
Derivative Time=0 - Decrease the Proportional Band to the point where a constant rate of oscillation is obtained. This is the response frequency of the system. The frequency is different for each process.
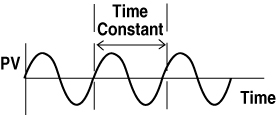
- Measure the Time Constant which is the time to complete one cycle of the response frequency. The Time Constant will be defined as "T" when calculating Integral and Derivative Times.
- Widen the Proportional Band until only slightly unstable. This is the Proportional Band's Ultimate Sensitivity. The Proportional Band's Ultimate Sensitivity width will be defined as "P" when calculating the actual Proportional Band.
- Use the following coefficients in determining the correct PID settings for your particular application.
| Control Action | P Setting | I Setting | D Setting |
|---|---|---|---|
| P Only | 2P | * | * |
| PI | 2.2P | .83T | * |
| PID | 1.67P | .5T | .125T |
